数值孔径NA和两个因素有关，一个是介质折射率，一个是图中的锥角a（也称孔径角），且都是成正比的关系。 
 
NA=介质折射率Xsin1/2 的开口角 
 
先来说说孔径角： 
 
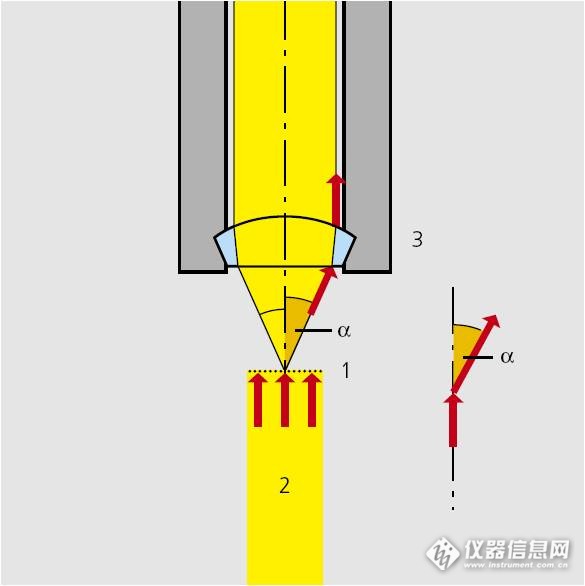
通俗点来说数值孔径的大小代表了一个物镜收集物体散射出来的光的能力的大小。上图中的物镜只能够收集锥角a之内的光线。我们知道，一个物体的细节越小（或者说他的空间频率越高），它散射的光的角度范围就越大。一个理想的物镜，应该能够收集所有角度的光线然后再在像面上还原出物体的像。但实际因为物理尺寸的限制，这个角度a总是有限并且小于90度的。也就是说那些包含在大于锥角a的散射光中的物体的高频细节信息损失掉了。那么能不能再改进一些呢？看下图： 
 
 
 
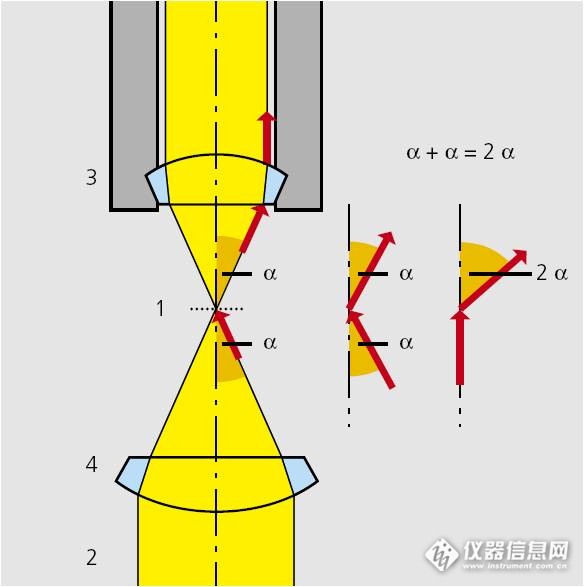
如果照明光不像第一图中那样是平行光，而是一个由聚光镜4产生的光锥，那么有可能收集到大于角度a的等效散射光线，这时同样的物镜可以还原更多的物体细节。所以物镜的分辨率应该是： 
 
 
 
        分辨率同时受到物镜和聚光镜数值孔径的限制，物镜的数值孔径越大分辨率越高。那么聚光镜的数值孔径是不是也越大越好呢？也不是，当聚光镜的NA和物镜的NA相同时，分辨率最高。为什么？因为当聚光镜的NA大于物镜时，超出的那部分大角度的光在物体上的零级散射（就是透射光）是不能被物镜收集的，只有大于零级的散射光能被收集，而这些光是不能有效的成像的（至少对明场成像是如此）。所以聚光镜的NA超过物镜时就没有实际意义了。我们从上面的图上还可以知道，最好物面1处每一点的照明都是这样的一个光锥，并且这个光锥的角度最好是可以根据不同物镜可调的。而这些正是科勒照明所能够满足的条件。 
        从上面的讨论可以知道，聚光镜在显微镜成像系统中也是一个限制因素，为了获得最佳的成像效果和发挥高NA物镜的能力，我们的显微镜上最好有一个高质量的聚光镜，并且要调整照明光路满足科勒照明条件。 
 
        在说说介质折射率： 
 
 
 
        而在显微镜系统中，对于给定的物镜，孔径角已经固定，若想增大其NA值，唯一的办法是增大介质折射率n值。因为空气的折射率永远都是小于1的，所以介质的折射率n值要大于1，就需要引入其他的介质比如油和水，NA值就可能大于1。 
 
数值孔径最大值为1.4（油），这个数值在理论上和技术上都达到了极限。目前，有用折射率高的溴萘作介质，溴萘的折射率为1.66,所以NA值可大于1.4。不过NA大于1.4的，我暂时还没见过和用过。